Noget om at gøre arbejdet ordentligt…
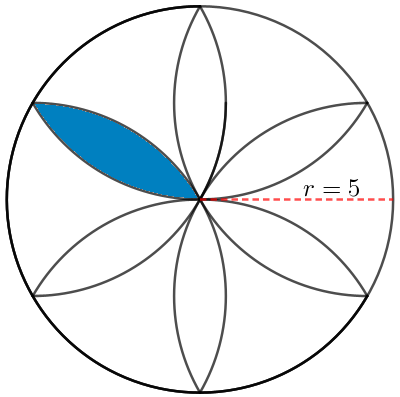
Vi sad nogle stykker i klasseværelset, 8. klasse, 7 elever og jeg helt nøjagtigt, og kiggede på en opgave fra matematikbanken – du kender den sikkert godt; beregn arealet af blomsterbladet i cirkeltegningen.
Vi sloges med forskellige elevers løsningsmodeller, der alle på en eller anden måde løb ud i sandet. Derfor så vi på, hvilke hints matematikbanken havde givet os. De skrev, at man skulle tænke i trekanter, og benytte GeoGebra til at tegne en trekant, for at finde blomsterbladets areal.
En metode til at løse opgaven med den information, var derefter nem nok at gennemskue, lige indtil en elev (gud ske tak og lov) sagde; »ja men der står beregn, Jesper!« Der blev lidt stille, og så måtte vi jo diskutere, hvad så nu – med vores nye erhvervede viden, kunne vi så beregne arealet. Inde i mit hovede begyndte jeg at tænke, at vi skal anvende Herons formel, men eleverne fandt frem til en lige så elegant, hvis ikke bedre metode.
Vores klasseværelse er klistret til med whiteboards, så vi benytter os gerne af at ‘tegne på væggene’, og her fandt en af eleverne ud af, at vi jo kunne benytte os af arealet af en sekskant – vi havde netop haft om arealer af regulære plane polygoner.

Vi ved, hvordan ‘blomsten er konstrueret’; ud af syv cirkler, alle med en radius på fem, derfor må afstanden mellem spidsen af blomstens blomsterblade, ligeledes være fem. Vi ved også at selve blomsterbladets længde, svarer til cirklens radius, altså også 5 .
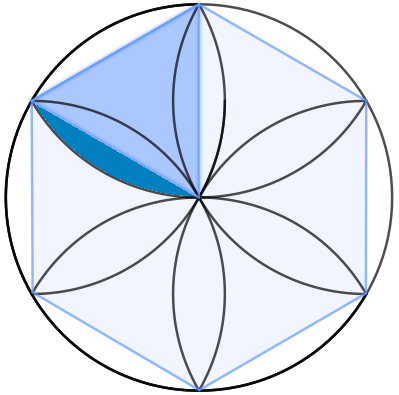
Hvis det forholder sig sådan, må arealet af cirkelafsnittet over trekanten, svare til arealet af det halve blad (lige nu havde de en meget stolt matematikunderviser) fordi det er en del af bladet i den anden cirkel.

Så derfor, blev konklusionen, at vi ved at trække sekskantens areal fra cirklens og dele med seks og gange med to, ville få arealet af et blomsterblad. Udregningen i Maple kom til at se således ud;
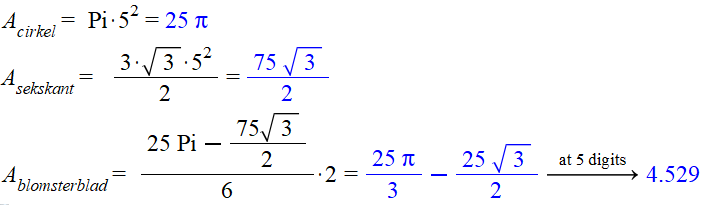
Jeg har tilladt mig at tilføje lidt tekst til deres beregninger, men ellers … godt gået. Man kan sige, at selv om lektionen gik ud over den tid vi havde til rådighed, var den givet godt ud. Eleverne var stolte, de havde beregnet en løsning, ikke tegnet en løsning – de havde gjort deres arbejde ordentligt. At de så lige så godt kunne have brugt argumentet om, hvordan størrelsen af blomsterbladet havde forholdt sig, ved at tegne en regulær trekant, er lige meget i denne sammenhæng.
Nu spørger du sikkert dig selv; kunne denne opgave både have været tegnet og beregnet i Maple? Selvfølgelig, men vejen derhen er analytisk og ikke ligefrem. Det kræver et kendskab til Maples pakker.
Herunder begynder jeg at finde skæringspunktet mellem to cirkler med radius fem med centrum i (0,0) og (5,0), for at bruge dette skæringspunkt som basis for de koordinater jeg vil tegne de seks cirkler, der ligger uden om centercirklen, fra.

En mere tricky udfordring, som jeg ikke ville give eleverne – i folkeskolen er GeoGebra helt fin og mere intuitiv til den type opgaver. Argumenter og udregningen af blomsterbladets areal, ville være den samme som oven over.

Hilsen Jesper


