Vi er glade for at se dig!
Vi er glade for at se dig!
I forlængelse af nedenstående lille oplæg om brug af CAS i det tænkende klasserum, først et hint: tænk i firkanter.
Forestil dig en retvinklet trekant, hvis areal er 30 og hvis omkreds er 30, hvor lang er da hypotenusen?
Selv om der kun er et facit, angiver undersøgelsesfasen to muligheder – men hvilken er den rigtige?
Måske findes tiden ikke iflg. kvantefysikerne. Tiden er bare en opdeling af tilværelsen i små organiserede bider, der alene tjener til at gøre en kompleks verden overskuelig. Den klassiske fysik ser tid som en lineær og uafhængig enhed, der bevæger sig fremad som en ensartet strøm, mens kvantemekanikken mener, at tid og rum er sammenflettede og afhængig af den der observerer, og i øvrigt; hvordan kan en partikel være to steder på samme tid?.
Jeg har været lærer og beskæftiget mig med undervisning så længe, at jeg hører gentagelsernes ekkoer prøver at snyde og lyde som fornyelse. Jeg plejer spøgefuldt at sige, at jeg rider på den tredje bølge. Spejlet afslører hver morgen den lineære tidsopfattelse, mens gentagelserne på en måde er undervisningsverdenens svar på kvantefysikken. Men sådan er det vel, en ny generation af undervisere skal vel også (gen)opfinde sig selv.
Det Tænkende Klasserum er endnu et (nyt) bud på en undervisingsstrategi, der bygger på et forskningsgrundlag så småt, at det ikke kan klassificeres som en videnskabeligt funderet teori, men alligevel sælges metoden som en revolutionerende religion. At vi ikke stopper op og kigger os undrende om kan overraske. Hvis vi bare skruer tiden lidt tilbage kan vi (måske) erindre de Mange Intelligenser, med en lige så tyndt videnskabelig baggrund, feje alle pædagogiske betænkeligheder og erfaringer af banen, på trods af at Howard Gardner selv advarede, at sådan kunne hans teori ikke anvendes.
Hvad forskningen og årtiers empiri kan underbygge, er seks evidensbaserede læringsstrategier, man ved virker; spaced practice, interleaving, retriveal practice, elaboration, concrete examples og dual coding.
Hver for sig fremmer de seks læringsoptimerende strategier elevernes læringspotentiale, men udnyttes de i kombination med hinanden øges læringspotentialet yderligere.
Det Tænkende Klasseværelse er på en måde eventyret om suppestenen, en charlatans manipulation af en landsby. Han fortæller han kan lave “suppe på en magisk suppesten.” Han begynder at koge vand med stenen i, og langsomt bliver landsbyboerne nysgerrige. En efter en bringer de ingredienser som kartofler, gulerødder, og kød, til gryden. Til sidst har de sammen skabt den velsmagende suppe.
Moralen er, at ved at dele og samarbejde i et kraftfuldt fællesskab kan man opnå mere, end man kan alene.
Suppestenen er den vertikale slet- og skrivbare tavle, mens landsbyens ingredienser er dine ideer i kombination med mindst tre af de ovennævnte (indfarvede) evidensbaserede kognitive læringsstrategier, og min påstand er her, at det er de sidste ingredienser der får læringsstrategien bag det tænkende klasserum til at virke, og ikke whiteboards på ben eller væg.
Retrieval practice, elaboration og concrete examples bygger alle på at dele, at samarbejde og på fællesskabet, Peter Liljedal præsenterer en god måde at kombinere disse tre af de seks kognitive strategier (de vertikale flader), og det er derfor at hans strategi vil fungere (for en periode).
Har du læst det som et kritisk indlæg i forhold til Det Tænkende Klasseværelse, tager du fejl – kast dig ud i det, afprøv det og skab din egen version af en udmærket vision, læs endelig hans bog og bliv inspireret til nye vinkler på din undervisning. Men vær kritisk!
Jeg fik for et par år siden en klasse til at mene at H. C. Branners De Blå Undulater var den mest spændende novelle de nogensinde havde læst, ved at brænde igennem og udvise troen på det. Peter Liljedal brænder for det og er selv aktivt deltagende i de klasser han bruger som grundlag for sine undersøgelser – derfor skal det lykkes, må det lykkes, for han definerer selv sine succeser.
Det er her min kritik tager sit udgangspunkt. Jeg har set nok tilfælde, hvor visionen er taget i brug men faklen tabes og slukkes når nyhedens interesse hos eleverne har lagt sig, og det at stå op også er blevet hverdag – så er vi tilbage i de seks strategier og dine gode ideer. Vores mål er ikke hans mål, vores mål er blandt andet defineret af de nationale læringsmål og andre udefra kommende udfordringer, der også skal tages hensyn til.
Så min afsluttende opfordring herfra er selv at kombinere de seks læringsstrategier og blive ved med at inspirere eleverne med nye tilgange, når interessen for Det Tænkende Klasseværelse ebber ud. Altså, fyld gammel vin på nye flasker!
Mangler du en opgave i trigonometri til dine elever, er du mere end velkommen til at benytte nedenstående og selv skrive den historie med de opgaver, i et sprog som du finder dine elever kan forstå.
De fleste ville mene, at pile på akserne i et koordinatsystem er standard. De markerer de positive retninger på både x-aksen og y-aksen og viser, at akserne fortsætter mod det uendelige. Maple tegner som standard ikke pile på akserne i deres koordinatsystemer. Dette skyldes, at Maple fokuserer på at give en ren og enkel visning af grafer, hvor pile ikke altid er nødvendige for at forstå grafens indhold.
Hvis du alligevel insistere på at elevernes koordinatsystemer skal indeholde pile for både x-akse og y-akse, kan de heldigvis tilføjes nemt.
Start med at klikke på grafen og i værktøjslinjen, hvor der står plot skal du i stedet vælge Drawing
Nu åbner en ny værktøjslinje, fordi at Maple nu behandler din graf som et billede. Du har nu mulighed for at tilføje forskellige elementer såsom at tegne på grafen og tilføje tekst. Det sidste vil vi gøre nytte af. Vi kan tilføje tekst der fungerer som pile og flytte teksten derhen, hvor vi vil have den. (Du kan opnå en pænere pil, hvis du har numerisk tastatur og holder [Alt] nede samtidigt med du skriver 30 (▲) )
Man drejer et objekt, det være sig en tegning eller en tekst, ved at have klikket på pilen (flyt) og holde [ctrl] nede mens man holder musen til hjørnet af figuren. Når du drejet figuren kan du flytte den hen, hvor den skal være og evt. finjustere med piletatsterne.
På samme måde tilføjes den x-aksens pil. Du kan også tilføje navne til akserne på denne måde. Når du skal arbejde videre, klikker du bare uden for tegningen, og fortsætter som før.
Flere steder har man blæst til angreb på den traditionelle didaktiske tilgang til matematikundervisningen, det være sig den håndholdte og guide tour de force gennem et curriculum, fastlagt enten af et bogsystem, en automatisk generet årsplan fra en digital platform eller kommunal målstyring. Den grundlæggende idé er at skabe og strukturere et miljø, hvor eleverne er tvunget til at tænke, fordi de ikke har andet valg.
Målet med en ny didaktiske tilgang er, at ved at fremme eleverne tænkning, lærer de mere og vil derfor klare sig bedre i matematik. Skiftet i den didaktiske tænkning og strukturering, og den dialog der pågår er opstået i kølvandet på bogen Det Tænkende Klasseværelse udgivet 2017 af Peter Liljedahl. Samtidigt har vore nuværende undervisningsminister bebudet et opgør med digitaliseringen af undervisningen, og vil have »mere papir, og færre skærme i skolen« i et forsøg på at prioritere analog undervisning og begrænse brugen af skærme.
Spørgsmålet der står tilbage er; er der plads til CAS i det tænkende klasseværelse?
Peter Liljedahl baserer sin bogs konklusioner ud fra observationer af 40 forskellige matematikklasser, fra børnehaveklase til 12. klasse, og det han bemærkede var, at uanset niveauet, så han elever der ikke tænkte og lærere der planlagde deres undervisning ud fra et princip om at håndholde og guide eleverne gennem et curriculum, altså, mente han, måtte underviseren gå ud fra, at eleverne ikke kunne eller ville tænke selv. (… og alle steder fandt jeg det samme – elever der ikke tænkte selvstændigt og lærere, der basserede deres undervisning på antagelsen om, at eleverne enten ikke kunne eller ville. s. 21 -22)
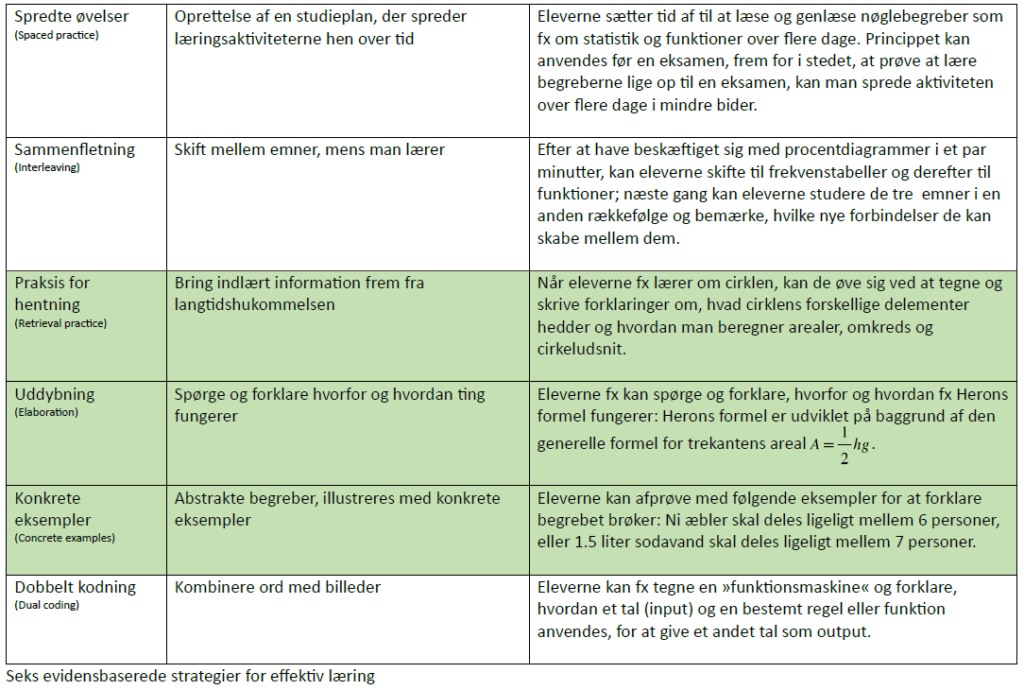
Så i løbet af de næste 15 år arbejdede han sammen med et team af undervisere, med det ene formål at finde ud af, hvordan man kan øge antallet af elever der tænker, og den tid, de bruger på at tænke. Resultatet blev fjorten praksisser, der når de er sat rigtigt sammen, opbygger et tænkende klasseværelse. Tænkning er en nødvendig forudsætning for læring, for, hvis elever ikke tænker og dermed fordyber sig, lærer de ikke – den anvendte viden de netop har tilegnet sig, bliver skubbet væk af det næste de beskæftiger sig med og glemt.
Målinger har vist, og det kommer ikke som en overraskelse hos os der arbejder med eleverne, at det modtage og koncipere matematik, kommer med en masse udfordringer for eleverne. Men vi er overbeviste om, at når det kommer til læring, kan vi gøre oplevelsen bedre, og opnå flere niveauer af læring og kritisk tænkning samt øge engagementet, når muligheder i CAS kombineres med de fjorten principper for det tænkende klasseværelse.
De 14 principper er designet til at udvikle elevernes selvstændige og undersøgende praksis, til fremme af tænkning og samarbejde om løsninger, men Liljedahl påpeger samtidigt, at man kan opnå stor effekt ved bare at bruge tre af dem;
De 14 principper er designet til at udvikle elevernes selvstændige og undersøgende praksis til fremme af tænkning og samarbejde om løsninger, men påpeger samtidigt at man kan opnå stor effekt ved bare at bruge tre af dem.
Som et eksempel på tre brugbare praksisser man kan kombinere sammen med anvendelsen af CAS, kan vi starte med princip 4, der opfordrer til at formulere mundtlige opgaver, frem for skriftligt, og få eleverne til at udføre opgaven inden for fem minutter af en lektion. Det har, ifølge Liljedahl, vist sig, at ved at gøre dette, producerer eleverne mere differentieret tænkning end ved at give dem opgaven senere.
Princip 5 – begynd lektionen med indholdsrige opgaver – fortæller os, at hvis målet er, at vores elever skal udvikle en faglig tænke-kultur, er vi nødt til, at give dem noget at tænke på, ved at give dem motiverende og engagerende, ikke lærerstyrede opgaver på forhånd og gå over til læseplanen senere.
Princip 6, mobiliser viden, henviser til, at for virkeligt at få adgang til den viden der ligger i en tænkekultur, skal eleverne lære at anvende og anerkende deres samarbejdspartners viden, gøre brug af den viden der findes i rummet, hos fx deres klassekammerater, og mobilisere den viden for at holde sig selv i gang som tænkende bidragsyder når de går i stå.
Hvis du sidder, mens du læser dette, og tænker, hvordan du kan implementere CAS sammen med det tænkende klasserum, kommer her et par ressourcer og tips til, hvordan du kan bruge nogle af disse principper i din undervisning.
En af de vigtige nøgleprincipper, er at eleverne skifter samarbejdspartnere ofte for at udfordre deres måde at tænke på, altså princip 3. Der er flere gratis værktøjer og hjemmesider der tilbyder at danne grupper. En webside der tilbyder flere forskellige gratis værktøjer er classtools.net, herunder en gruppedannelse-generator og tilfældigt valg af elev. Starter man her med at danne tilfældige grupper, er man i gang.
Liljedahl opfordrer til, at man generere gruppedannelserne synligt og tilfældigt, og ved at gøre det mens at eleverne ser på, sikrer man sig at eleverne faktisk oplever og bliver overbeviste om, at grupperne er tilfældige, og, siger Liljedahl, der har den effekt at eleverne begynder at se sig selv som værdifulde bidragsydere i tænkefællesskabet, der er i stand til matematisk tænkning.
Hver gruppe udstyres med en computer med et CAS-system. Vi anbefaler at den undersøgende opgave allerede ligger tilgængelig, eller kan hentes ind i CAS-systemet af eleven. Ideen er, at eleverne læser opgaven, derefter går i par, til nød tre, en rute der er aftalt på forhånd.
I de to – tre minutter turen varer, diskuterer eleverne mulige løsningsmuligheder og returnerer til deres CAS-system for at afprøve, hvad de har diskuteret sig frem til.
Opgaven kunne fx være; hvor lidt gavepapir skal jeg bruge til at pakke chokolade ind, når hver æske måler 2,5cm x 14cm x 14 cm?
Anvender eleverne Maple, kunne opgaven evt. udvides med, at løsningsmulighederne skulle præsenteres i programmets indbyggede slide-show.
»The-walk-and-talk« er et alternativ til at stå ved den lodrette flade, og stiller helt andre abstraktionskrav til eleverne. Metoden er et godt supplement til de tænkende klasserum, og sat sammen med et tidskrav udfordrer det ligeledes eleverne til at tænke og kommunikere med hinanden på en anden måde
Der kan opfindes, og der er mange undersøgende opgaver tilgængelige, der kan gøres til genstand for en walk-and-talk – metoden.
Flere CAS-systemer indeholder allerede opgavetyper, der lægger op til princip 4. Fx findes i Maple Applikationcenter og Maple Learn såkaldte gallerier, der kan bruges til fem-minutters tænkegymnastikken, fx The Physics of Santa Claus, Nonogrammer, Rubriks Cube eller Sudokuer.
Nogle af applikationerne kræver tankegang på tværs, som The Physics of Santa Claus, hvor man beskæftiger sig med, hvor hurtigt Julemandens rensdyr skal rende, for at han kan nå at kravle ned i skorstenen, spise de fremsatte kiks og drikke et glas mælk samt lægge julegaverne under træet, kravle op igen og flyve videre.
Andre applikationer, som et nonogram eller en sudoku kræver en anden form for logik og kommunikation, mens Rubriks Cube igen udfordrer logikken og dermed samtalen.
Ideen kunne være, at eleverne sidder i grupper af to eller tre, og prøver at løse opgaverne. Det kan gøres på mange måder. En af måderne ligger i princip 6. Lad den ene elev være dukkefører og den anden dukken, dukkeførerens opgave er det at kommunikere, hvad han eller hun tænker, og derigennem styre dukken mod en mulig løsning. Dukkefører og dukke skifter position hvert 3. minut. På den måde lærer de at kommunikere matematisk tankegang.
Princip 2 – brug lodrette sletbare flader, anses næsten som den hellige gral i det tænkende klasserum. Eleverne skal stå op og diskutere matematik, ikke bare sidde ned og løse opgaver. Et af de ting det tænkende klasserum tilskynder, er, at eleverne ser på andres arbejde, og når de sidder fast kan de se, hvordan andre arbejder med problemet. Det er sådan at viden mobiliseres på tværs af det tænkende klasserum. Det er en dimension der unægtelig er svær, når man sidder med et CAS-system på en lille computer.
Mobiliseringen kan fx løses ved, at alle grupper fx arbejder på digitale whiteboards, fx på miro.com, hvor alle har adgang, eller ved at kombinere de lodrette flader med undersøgende aktiviteter i et CAS-system, men hvor eleverne er forpligtiget til at skrive, hvilke spørgsmål de stiller sig selv og hvad de undersøger på de lodrette flader.
Det tænkende klasserum er et værdifuldt bidrag til matematikundervisningen, og selv om det er en mulighed for at motivere med engagerende indhold, skal vi som matematikundervisere også forholde os til de andre aspekter som vi er pålagt at undervise, såsom regneark, geometriske tegneprogrammer og CAS-systemer.
Det tænkende klasserums styrke, er at det gør eleverne aktive og deltagende i egen læring, hvor de samarbejder med deres jævnaldrende. De bruger deres kommunikation som en del af læringen, hvilket fremmer trivslen og skaber en større følelse af fællesskab. Så brug CAS og de digitale hjælpemidler som en del af det tænkende klasserum.
Til dem der foretrækker dette, er her fire videovejledninger. Til dem der foretrækker en »papir-udgave« er der en PDF-udgave til download og udskrift.
Installer Maple (video)
Installer Skolepakken (video)
Opret en Maple-konto (video)
Få adgang til din konto (video)
Installationsvejledning (PDF)
