Programmering i matematik del 2

Programmering med CalcMe

Egentlig burde det være oplagt at programmere i CalcMe. I paletten til venstre finder vi menupunktet Programmering. Hurtigt finder du ud af, at det er næsten så lige til, som det ser ud., for heldigvis er der god hjælp at hente i deres hjælpe-menu (desværre er denne del af hjælpemenuen endnu ikke oversat til dansk, men er kun tilgængelig på engelsk).

Åbner du for menupunktet, ser du de ni tilgængelige kommandoer og sløjfer, du kan anvende. (if, else, else if osv.) Lad os prøve, at programmere os igennem at løse en ligning, lige som i første del, hvor vi anvendte henholdsvis Basic og Google Sheets.

Øvelsen går ud på, at få programmet til at løse en lining i formen ax+c=d, fx 2x+5=9. Formålet er, at eleven bliver bevidst om, hvad det er man undersøger når en ligning løses.

Programmet:

Først skal vi have defineret variablen x, dvs give den en startværdi, fx x=-10.

Derefter anvender vi kommandoen repeat (gentag), og fortæller programmet at det skal lægge et til værdien af x indtil (until) at løsningen er fundet. I dette tilfælde x = 2.
Der er også andre løsninger, men denne er den hurtigste. (Du kan også bede CalcMe finde løsninger med decimaltal, ved fx at sætte x=x+0.1)

Programmering i Maple

Programmering i Maple følger sin egen programmeringssyntaks. Vi undersøger samme problemstilling; at få programmet til at løse en ligning af formen ax+b=c.
Måden vi anvender, kalder på lidt forarbejde fra eleverne, hvilket ikke gør noget i processen omkring at blive bevidst om, hvad det er man gør når man løser en ligning!

Først kigger vi på, hvorledes vi generelt finder løsningen frem på en ligning (hvordan vi finder x)
 ax +b = c \rightarrow \frac{c-b}{a}=x
og i vores eksempel med 2x+5=9
 2x+5=9 \rightarrow \frac{9-5}{2}

Programmering i Maple, der løser denne simple ligning bliver således;

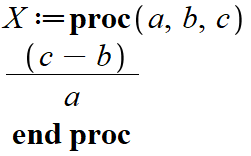
… og løsningen af ligningen 2x + 5 = 9, således

Til forskel til det programmeringseksempel vi har behandlet, kan dette lille program behandle alle simple ligninger, men der er også gået en anden slags forarbejde forud. Hvor vi i de tre første eksempler beskæftigede os med at undersøge, hvad der skete, hvis satte en bestemt x- værdi ind i ligningen, så beskæftiger vi os i Maple med selve mekanismen bag løsningen af en ligning.

Kodens struktur er opbygget af 3 elementer
1. proc (liste over parametre der indgår)
2. body (hvad skal programmet gøre)
3. end proc;

Lad os skrive en procedure ved at følge den beskrevne struktur som oven for.

1. liste over parametre   X := proc(a, b, c)
2. udregning (body)              (c – b)/a
3. Afslut programmet            end proc;

Lad os finde løsningen for ligningen 2x + 5 = 9:
X(2, 5, 9) = 2

Lad os finde løsningen for ligningen 3x – 1/8 = 5
L(3, 1/8, 5) = 13/8  etc …

På samme måde, kan man lade eleverne arbejde med at skrive procedure, altså programmer, der løser ligninger af typen ax + b = cx + d eller ya = bx + c ∧ yd = ex + f eller de Pythagoræiske tripler
(t*a)^2 + (t*b)^2 = (t*c)^2;

Det er giver efter vores mening mere mening, at eleverne først beskæftiger sig med den generelle løsningsform i stedet for ‘bare’ at lade programmet løbe en række tal sammen. Men smag og behag.

Du behøver ikke at stoppe her! Lav fx et program der kan udregne arealet af en trekant, hvor højden og grundlinjen er kendt, eller hvad med udregning af en trekants areal efter Herons formel, hvor længden af de tre sider er kendt?

Du kan finde alle eksemplerne under menupunktet Materialer \rightarrow Programmering i Maple

Rigtig god fornøjelse.